五度圏図と音程
音律で重要な五度や長三度といった音程を、五度圏図から読み取る方法を説明します。
五度圏図 ──── というくらいなので、隣に並んでいる音(F-C、C#-G#など)は五度です。
五度音程は全部で12ありますね。
長三度(C-Eなど)は、基準の音から右回りに四つ目になります。
長三度同士を線で結んでいくと、これも全部で12あることがわかります。
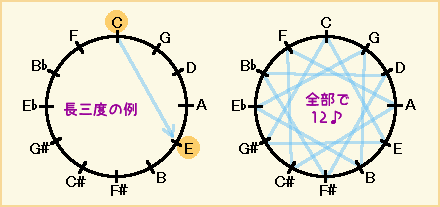
全ての五度と長三度が純正で、この五度圏の円がきちんと閉じていればいいのですが、世の中?はそんなに甘くないのでした。
例えば今、Cから始めて⇒G⇒D・・・と順に五度を純正(振動数2:3)に取りながら音を決めていくとします。
(どんどん音が高くなるので、適宜オクターブ下げる)
・・・B♭⇒Fと来たら、このFと最初にスタートしたCが純正五度になっていればいいですね。
しかし残念ながら、そうはならないんです!
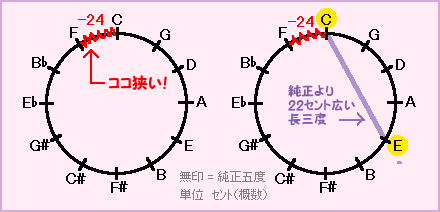
F⇒CのC音は、最初のCより約24セント(平均律半音=100セント)も高い!
しかし1オクターブを12音と限ると、もうこれ以上音を増やせないので、最後のF-Cは純正より約24セントも狭い五度になってしまいます。
これが音律第一の問題、五度の困った(笑)です。
次に、C⇒G⇒D⇒A⇒Eのように、純正五度を四つ積み重ねてできる長三度(G-B、D-F#なども同様)は、純正(振動数4:5)より約22セントも広くなってしまうのです!
これが音律第二の問題、長三度の困った(爆)です。
これらのことから ────
★五度音程の合計が -24セントで、五度圏の円が閉じる
★合計で -22セントになる五度を四つ積み上げた長三度は純正
・・・と言えます。
そこで練習問題!\(^ ^)/~~♪
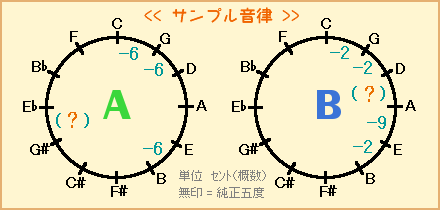
サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問1】( )内のセント値は?
【問2】純正長三度はいくつあるか?(無ければゼロで)
【問3】最も広い長三度は純正より何セント広いか?
解答は次の記事で♪
五度圏図 ──── というくらいなので、隣に並んでいる音(F-C、C#-G#など)は五度です。
五度音程は全部で12ありますね。
長三度(C-Eなど)は、基準の音から右回りに四つ目になります。
長三度同士を線で結んでいくと、これも全部で12あることがわかります。
全ての五度と長三度が純正で、この五度圏の円がきちんと閉じていればいいのですが、世の中?はそんなに甘くないのでした。
例えば今、Cから始めて⇒G⇒D・・・と順に五度を純正(振動数2:3)に取りながら音を決めていくとします。
(どんどん音が高くなるので、適宜オクターブ下げる)
・・・B♭⇒Fと来たら、このFと最初にスタートしたCが純正五度になっていればいいですね。
しかし残念ながら、そうはならないんです!
F⇒CのC音は、最初のCより約24セント(平均律半音=100セント)も高い!
しかし1オクターブを12音と限ると、もうこれ以上音を増やせないので、最後のF-Cは純正より約24セントも狭い五度になってしまいます。
これが音律第一の問題、五度の困った(笑)です。
次に、C⇒G⇒D⇒A⇒Eのように、純正五度を四つ積み重ねてできる長三度(G-B、D-F#なども同様)は、純正(振動数4:5)より約22セントも広くなってしまうのです!
これが音律第二の問題、長三度の困った(爆)です。
これらのことから ────
★五度音程の合計が -24セントで、五度圏の円が閉じる
★合計で -22セントになる五度を四つ積み上げた長三度は純正
・・・と言えます。
そこで練習問題!\(^ ^)/~~♪
サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問1】( )内のセント値は?
【問2】純正長三度はいくつあるか?(無ければゼロで)
【問3】最も広い長三度は純正より何セント広いか?
解答は次の記事で♪
PR
♪この記事にコメントする♪
最新記事♪
カテゴリー♪
スポンサードリンク
ブログ内検索
最新コメント♪
スポンサードリンク
中の人より
管理人名:REIKO
★リンクはご自由に★
どのページでも構いません
★リンクはご自由に★
どのページでも構いません
