五度圏図で音律を見る
前回の五度圏図と音程の続きです ──── まず練習問題を再掲↓↓↓
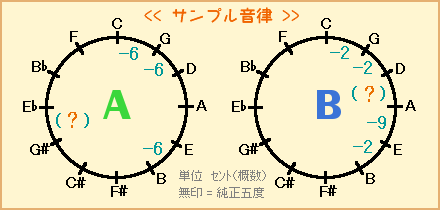
サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問1】( )内のセント値は?
【問2】純正長三度はいくつあるか?(無ければゼロで)
【問3】最も広い長三度は純正より何セント広いか?
前回の説明で、純正五度を積み上げて音を作っていく時、最後に「行き過ぎてしまう」約24セントをピタゴラス・コンマ、純正五度四つでできる広い長三度と純正長三度の差、約22セントをシントニック・コンマと言います。
(どちらのコンマも、比を使い分数で表すか小数値の方が正確ですが、最初からそれを使うと分かりにくくなるので、整数値の概数で話を進めます)
それぞれが「行き過ぎ」「広すぎ」た分をマイナスすれば、五度圏が閉じたり純正長三度ができたりするわけですね。
それを踏まえて ──── では解答♪
【問1】A・・・-6、B・・・-9
全部で-24になればいいので簡単ですね。
間違えた人は、中学時代「正の数・負の数」の授業で寝てたでしょ?(爆)
【問2】A・・・ゼロ、B・・・2
A音律は、最も純正に近い長三度(例えばC-E)でも、純正より10セントも広いです。
B音律は、C-EとG-Bがそれぞれ-22セントで純正長三度。
【問3】A・・・16セント広い(D-F#など、間で6セントしかマイナスしてない箇所)
B・・・22セント広い(B-E♭など、間が全て純正五度の箇所)
問3が少し難しかったかもしれませんが、皆様の結果はどうでしたか~?\(^-^*)
音律AはベンデラーIII(1690頃)、Bはキルンベルガー第二法の修正版(1776)です。
前者はピタゴラス・コンマを四分割した音律という点で、有名なヴェルクマイスター(第一技法第三番)と似ていますが、狭い五度の配置が違います。↓↓↓
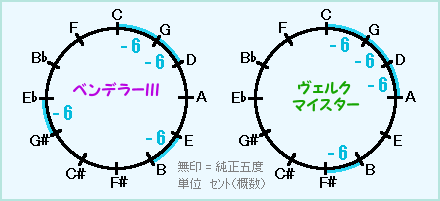
狭い五度が五度圏の右半分に集まっているヴェルクマイスターよりも、バラけているベンデラーの方が均(なら)された音律と言えます。
ベンデラーの狙いは、純正五度を四つ積み上げた純正より22セント広い長三度(いわゆるピタゴラス長三度⇒長三度の和声としては広すぎ、不快な響き)を無くすことにあったのでしょう。
特定の調よりは全調向けの構成で、バッハの平均律クラヴィーア曲集をこれで通すのもアリな音律と思います。
キルンベルガー第二法とその修正音律を比べると ──── ↓↓↓
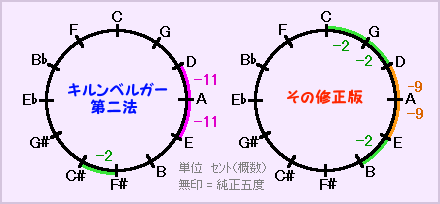
第二法の純正より11セント狭い五度がガマンならない?ので、2セントずつ削ってC-G-Dに配したんでしょうね・・・しかしそうすると、G-Bの純正長三度が失われるので、F#-C#にあった-2セントをE-Bに移動させたと思われます。
一体誰ですかね~、こんなしみったれた(笑)修正をしたのは!?
(キルンベルガー本人の修正か、第三者によるものかは調べてないので分かりません)
五度の調整はプラスマイナス6セントほどが「限度」、それ以上だと不具合の原因になるので、修正しようとした気持ちは理解できますが、依然として9セント狭い五度が残っているんじゃ中途半端な気がしますけど。(^ ^;)
・・・というように、数値データを並べただけではチンプンカンプンの音律も、五度圏図に表すと一杯やりながら?あ~だこ~だとうんちくを傾けられるようになるのです。
ぜひ五度圏図と仲良くなってください♪
サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問1】( )内のセント値は?
【問2】純正長三度はいくつあるか?(無ければゼロで)
【問3】最も広い長三度は純正より何セント広いか?
前回の説明で、純正五度を積み上げて音を作っていく時、最後に「行き過ぎてしまう」約24セントをピタゴラス・コンマ、純正五度四つでできる広い長三度と純正長三度の差、約22セントをシントニック・コンマと言います。
(どちらのコンマも、比を使い分数で表すか小数値の方が正確ですが、最初からそれを使うと分かりにくくなるので、整数値の概数で話を進めます)
それぞれが「行き過ぎ」「広すぎ」た分をマイナスすれば、五度圏が閉じたり純正長三度ができたりするわけですね。
それを踏まえて ──── では解答♪
【問1】A・・・-6、B・・・-9
全部で-24になればいいので簡単ですね。
間違えた人は、中学時代「正の数・負の数」の授業で寝てたでしょ?(爆)
【問2】A・・・ゼロ、B・・・2
A音律は、最も純正に近い長三度(例えばC-E)でも、純正より10セントも広いです。
B音律は、C-EとG-Bがそれぞれ-22セントで純正長三度。
【問3】A・・・16セント広い(D-F#など、間で6セントしかマイナスしてない箇所)
B・・・22セント広い(B-E♭など、間が全て純正五度の箇所)
問3が少し難しかったかもしれませんが、皆様の結果はどうでしたか~?\(^-^*)
音律AはベンデラーIII(1690頃)、Bはキルンベルガー第二法の修正版(1776)です。
前者はピタゴラス・コンマを四分割した音律という点で、有名なヴェルクマイスター(第一技法第三番)と似ていますが、狭い五度の配置が違います。↓↓↓
狭い五度が五度圏の右半分に集まっているヴェルクマイスターよりも、バラけているベンデラーの方が均(なら)された音律と言えます。
ベンデラーの狙いは、純正五度を四つ積み上げた純正より22セント広い長三度(いわゆるピタゴラス長三度⇒長三度の和声としては広すぎ、不快な響き)を無くすことにあったのでしょう。
特定の調よりは全調向けの構成で、バッハの平均律クラヴィーア曲集をこれで通すのもアリな音律と思います。
キルンベルガー第二法とその修正音律を比べると ──── ↓↓↓
第二法の純正より11セント狭い五度がガマンならない?ので、2セントずつ削ってC-G-Dに配したんでしょうね・・・しかしそうすると、G-Bの純正長三度が失われるので、F#-C#にあった-2セントをE-Bに移動させたと思われます。
一体誰ですかね~、こんなしみったれた(笑)修正をしたのは!?
(キルンベルガー本人の修正か、第三者によるものかは調べてないので分かりません)
五度の調整はプラスマイナス6セントほどが「限度」、それ以上だと不具合の原因になるので、修正しようとした気持ちは理解できますが、依然として9セント狭い五度が残っているんじゃ中途半端な気がしますけど。(^ ^;)
・・・というように、数値データを並べただけではチンプンカンプンの音律も、五度圏図に表すと一杯やりながら?あ~だこ~だとうんちくを傾けられるようになるのです。
ぜひ五度圏図と仲良くなってください♪
PR
♪この記事にコメントする♪
最新記事♪
カテゴリー♪
スポンサードリンク
ブログ内検索
最新コメント♪
スポンサードリンク
中の人より
管理人名:REIKO
★リンクはご自由に★
どのページでも構いません
★リンクはご自由に★
どのページでも構いません
