音律の右脳改革鍵盤館♪

前回の五度圏図と音程の続きです ──── まず練習問題を再掲↓↓↓



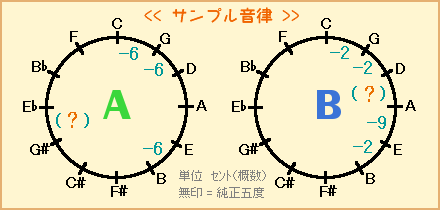
サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問１】（　　）内のセント値は？
【問２】純正長三度はいくつあるか？（無ければゼロで）
【問３】最も広い長三度は純正より何セント広いか？

前回の説明で、純正五度を積み上げて音を作っていく時、最後に「行き過ぎてしまう」約24セントをピタゴラス・コンマ、純正五度四つでできる広い長三度と純正長三度の差、約22セントをシントニック・コンマと言います。
（どちらのコンマも、比を使い分数で表すか小数値の方が正確ですが、最初からそれを使うと分かりにくくなるので、整数値の概数で話を進めます）
それぞれが「行き過ぎ」「広すぎ」た分をマイナスすれば、五度圏が閉じたり純正長三度ができたりするわけですね。
それを踏まえて ──── では解答♪

【問１】A・・・-６、B・・・-９
　　全部で-24になればいいので簡単ですね。
　　間違えた人は、中学時代「正の数・負の数」の授業で寝てたでしょ？（爆）
【問２】A・・・ゼロ、B・・・２
　　A音律は、最も純正に近い長三度（例えばC-E）でも、純正より10セントも広いです。
　　B音律は、C-EとG-Bがそれぞれ-22セントで純正長三度。
【問３】A・・・16セント広い（D-F#など、間で６セントしかマイナスしてない箇所）
　　　　B・・・22セント広い（B-E♭など、間が全て純正五度の箇所）
　　　　
問３が少し難しかったかもしれませんが、皆様の結果はどうでしたか～？＼（＾-＾*）
音律AはベンデラーIII（1690頃）、Bはキルンベルガー第二法の修正版（1776）です。
前者はピタゴラス・コンマを四分割した音律という点で、有名なヴェルクマイスター（第一技法第三番）と似ていますが、狭い五度の配置が違います。↓↓↓



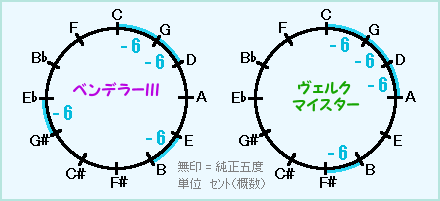
狭い五度が五度圏の右半分に集まっているヴェルクマイスターよりも、バラけているベンデラーの方が均（なら）された音律と言えます。
ベンデラーの狙いは、純正五度を四つ積み上げた純正より22セント広い長三度（いわゆるピタゴラス長三度⇒長三度の和声としては広すぎ、不快な響き）を無くすことにあったのでしょう。
特定の調よりは全調向けの構成で、バッハの平均律クラヴィーア曲集をこれで通すのもアリな音律と思います。

キルンベルガー第二法とその修正音律を比べると ──── ↓↓↓



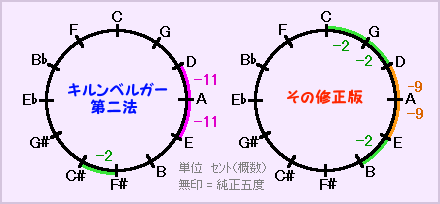
第二法の純正より11セント狭い五度がガマンならない？ので、２セントずつ削ってC-G-Dに配したんでしょうね・・・しかしそうすると、G-Bの純正長三度が失われるので、F#-C#にあった-2セントをE-Bに移動させたと思われます。
一体誰ですかね～、こんなしみったれた（笑）修正をしたのは！？
（キルンベルガー本人の修正か、第三者によるものかは調べてないので分かりません）
五度の調整はプラスマイナス６セントほどが「限度」、それ以上だと不具合の原因になるので、修正しようとした気持ちは理解できますが、依然として９セント狭い五度が残っているんじゃ中途半端な気がしますけど。（＾ ＾；）

・・・というように、数値データを並べただけではチンプンカンプンの音律も、五度圏図に表すと一杯やりながら？あ～だこ～だとうんちくを傾けられるようになるのです。
ぜひ五度圏図と仲良くなってください♪

音律で重要な五度や長三度といった音程を、五度圏図から読み取る方法を説明します。
五度圏図 ──── というくらいなので、隣に並んでいる音（F-C、C#-G#など）は五度です。
五度音程は全部で12ありますね。
長三度（C-Eなど）は、基準の音から右回りに四つ目になります。
長三度同士を線で結んでいくと、これも全部で12あることがわかります。



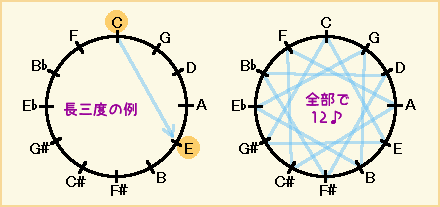
全ての五度と長三度が純正で、この五度圏の円がきちんと閉じていればいいのですが、世の中？はそんなに甘くないのでした。
例えば今、Cから始めて⇒G⇒D・・・と順に五度を純正（振動数２：３）に取りながら音を決めていくとします。
（どんどん音が高くなるので、適宜オクターブ下げる）
・・・B♭⇒Fと来たら、このFと最初にスタートしたCが純正五度になっていればいいですね。
しかし残念ながら、そうはならないんです！
F⇒CのC音は、最初のCより約24セント（平均律半音＝100セント）も高い！
しかし１オクターブを12音と限ると、もうこれ以上音を増やせないので、最後のF-Cは純正より約24セントも狭い五度になってしまいます。
これが音律第一の問題、五度の困った（笑）です。

次に、C⇒G⇒D⇒A⇒Eのように、純正五度を四つ積み重ねてできる長三度（G-B、D-F#なども同様）は、純正（振動数４：５）より約22セントも広くなってしまうのです！
これが音律第二の問題、長三度の困った（爆）です。



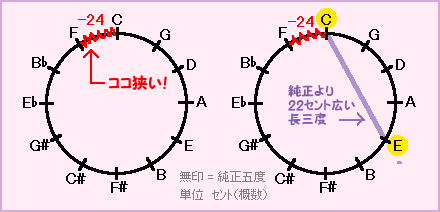
これらのことから ────
★五度音程の合計が -24セントで、五度圏の円が閉じる
★合計で -22セントになる五度を四つ積み上げた長三度は純正
・・・と言えます。
そこで練習問題！＼（＾ ＾）／～～♪



サンプル音律A・Bそれぞれについて、次の問いに答えなさい♪
【問１】（　　）内のセント値は？
【問２】純正長三度はいくつあるか？（無ければゼロで）
【問３】最も広い長三度は純正より何セント広いか？

解答は次の記事で♪

音律を図示してその構成を把握するのに便利なのが、時計のような五度圏図です。
現在では、コンピュータで三次元的に描画する方法もたくさん考案されていますが、何と言ってもこの五度圏図は、チラシの裏に鉛筆でも書ける気軽さが魅力！
これが理解できないと音律の理論も実践も難しいので、今回は五度圏図の基本を説明します。

まず円を書いて、円周を時計のように12等分します。
12時の位置から始めて、右回り（時計回り）に五度上の音を順に書き入れます。

ポイント：五度圏図は「右回り」に見るのが基本！

ここで問題になるのが、日本では色々な音名が使われてることですが・・・



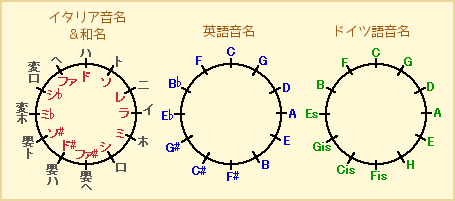
このブログでは、原則として英語音名で行くことにします。
C⇒G⇒D・・・と進んで、・・・F⇒Cで一周し、12の音が全て揃います。
A⇒B⇒C・・・と並んでいれば簡単なのに、なぜ五度間隔なんだ！と思いますが、この方法だと非常に便利なことがたくさんあるのです。
例えば ──── ハ長調音階の音が、どこに並んでいるか探してみてください。
またト長調音階ではどうでしょう？
こうなりますね♪↓↓↓



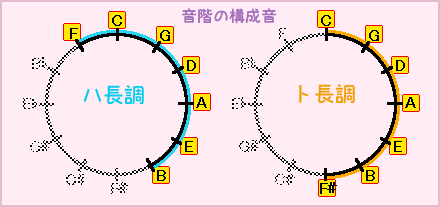
ポイント：長調の音階構成音は、主音の一つ左隣から順に半円状に並んでいる！

ハ長調⇒ト長調の転調は、五度圏を一つ右に回るだけ（FをF#に代えるだけ）なのが一目で分かります。
つまり五度上への転調が一番簡単＆自然なのは、音階の音を一つ取り替えるだけだから。
同様に五度下（ハ長調⇒ヘ長調）への転調も、一音だけの変更で済みます。
このように、主音が五度隣の調同士を（五度）近親調といいますが、五度圏図ではそれらが実際に仲良く並んでいるのです。

ト長調始まりの曲で臨時記号も少なければ、その曲は五度圏図の右半分の音中心に鳴っているので、この領域の音程（主に五度や長三度）が正しければ「美しく」聴こえるはずです。
まあ左半分は適当でもいい（笑）ってことですね。
ですが曲中、同名短調のト短調に転調したらどうなるでしょうか？
ト短調（自然的短音階とすれば）の構成音は、五度圏図の上半分になります。↓↓↓



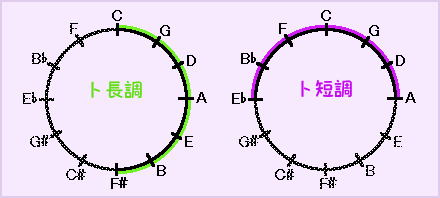
左側は適当・・・とは言ってられなくなりますね。（笑）
ある程度複雑で長い曲は、最初が何調であろうと曲中頻繁に転調して、五度圏を縦横無尽に駆け回っていることがほとんどです。
それでも楽譜を読んで五度圏図と照らし合わせてみると、「メイン領域」「出張（笑）領域」とか「左回りにどんどん転調」「十文字和音（C・A・F#・E♭）」など、色々と面白いことに気づきます。
音律は必ずどこかにしわよせを持っているので、このような見方が最適音律を見つける際の重要なヒントになるのです。